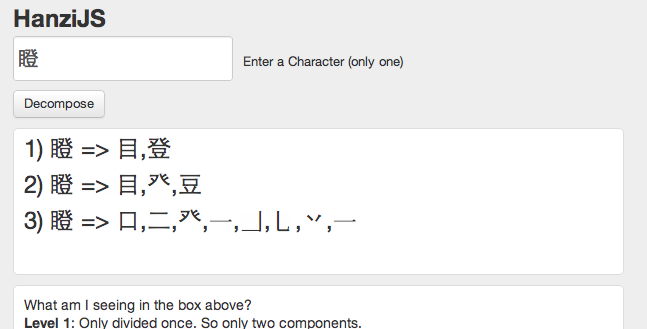
HanziJS is a tool that I created earlier this year to help me find the components (radicals) of Chinese characters. It was rudimentary at best, but I’ve finally taken time off to update it a bit more. It is part open-source project, part tool. A picture below showing how decomposition looks like now.

So what's new?

- It now decomposes the character a lot further. There has been a LOT of background changes in terms of code (check the GitHub project for more info).

- There are 3 levels of decomposition: Once, Radical & Graphical respectively.

Once justs decompose it into the two most obvious radicals. This helps for checking out for dictionaries or learning Chinese characters, especially phono-semantic compounds.

Radical decomposition decomposes the character into smallest possible "radical" components. This is based on the KangXi radical list. This can also be a good way to remember how to write characters. Sometimes Level 1 & 2 will show the same decomposition.

Graphical decomposition takes this a step further and goes down to lowest components, which will often be strokes or the last meaningful pieces. This is not necessarily in the right stroke order. This level of decomposition is still experimental, but still interesting to look at nonetheless.

- Redesign. I changed the design a little bit. Nothing big.

- Getting rid of "blocks" or glyph errors. I found a way to fix this. You need to download the correct font! This will allow you to see all the small things, like strokes or uncommon pieces.

So where to next?

- Add more information, like Pinyin & Definitions. The backend has this functionality already, but needs to be adapted for display purposes.

- Sentence segmentation (multiple characters). Dissect more than once character.

- API. I can create an API for people who'd want to use this. If you're interested contact me. I'm not sure yet how to approach this yet, but willing to talk.

- Your awesome idea!?

Yes, I'm looking for more cool ideas on how to improve HanziJS. Who you be willing to pay for extra cool features (like being able to compute the regularities as mentioned in this post)? Lemme know either way. I'd love to hear your feedback! Comment forth!

P.S. - I just like to say thanks to Gavin Grover again for providing the awesome data for the decompositions.